I. Funktionen und ihre Graphen
1.1 Funktionen
1.2 Verschieben und Strecken von Graphen
In die Eingabezeile oben kannst du direkt Funktionsterme eingeben ( z.B. x^2). Wenn es unübersichtlich wird, kannst du auf „neu laden“ (oben rechts) klicken.
Aufgabe 1: Potenzfunktionen mit rationalen Exponenten
Bearbeite das AB komplett in Geogebra!
1.3 Zusammengesetzte Funktionen
1.4 Verhalten für x gegen Unendlich
So, wie wir Zahlen addieren und subtrahieren Zahlen können, können wir auch Funktionen addieren und subtrahieren. Zum Beispiel, wenn wir Funktionen f und g haben, können wir zwei neue Funktionen schaffen: f + g und f – g. Weiterlesen
1.5 Symmetrie von Funktionen
siehe Geogebra-Buch
1.6 Nullstellen ganzrationaler Funktionen
1.7 Mehrfache Nullstellen
II Ableitung - Differenzielrechnung
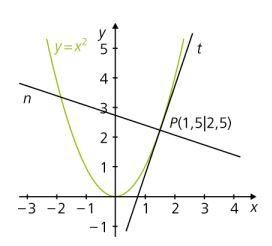
1 Differenzenquotient – mittlere Änderungsrate
2 Ableitung momentane Änderungsrate
3 Die Ableitungsfunktion
5 Die Ableitung von Potenzfunktionen - Potenzregel
2. Ableitungsregeln
1) Stelle eine Tabelle mit n und den Funktionstermen von f und f‘ auf
2) Verändere die Hochzahl n und skizziere zuerst in Gedanken f'(x). Kontrolliere Dein Ergebnis.
3) Wie sieht der Funktionsterm von f und f‘ aus? Übertrage die Ergebnisse in Deine Tabelle.
4) Kann man für die Ableitungsfunktion f‘ eine Regel erkennen? Stelle eine Vermutung auf!
5) Kontrolliere Dein Ergebnis, indem Du die Ableitung für beliebiges a berechnest. Kontrolliere Dein Ergebnis (Schieberegler)
6) Verändere nun den Faktor a und wiederhole die Schritte 1 – 5!
Übertrage nun den Merksatz in Dein Schulheft.
Weitere Hilfen: